 |
| Introduction |
| Symmetry Elements |
| · Proper Rotation Axis |
| · Mirror Plane |
| · Inversion Centre |
| · Improper Rotation Axis |
| · Identity |
| Point Group Gallery |
| Spotting a Chiral Compound |
| · Part I - Mirror Planes |
| · Part II - Inversion Centre |
| · Part III - Improper Rotation |
| · Summary & Conclusion |
| WSM Homepage |
Molecular Symmetry and Chirality
How to Spot a Chiral Compound
Note: viewing the structures on these pages requires use of
the MDL Chime Plug-In.
| Part III - Improper Rotation | [Part I] [Part II] [Summary] |
In very nearly all cases, lack of both a mirror plane and an inversion centre means a compound is chiral. But not always. In other words, lack of both σ and i is necessary for chirality, and very nearly sufficient, but not quite.
The most precise and succinct requirement for chirality is the lack of any Sn rotation axis. Lack of Sn is both a necessary and sufficient condition for chirality. However, all odd-value Sn axes require the presence of a σ, and an S2 axis is equivalent to i, so the lack of both an inversion centre and a mirror plane almost always amounts to a lack of Sn. Strictly speaking, it is possible for a molecule to lack both i and σ and still remain achiral: it must belong to an even-value Sn point group with n > 2. This is exceptionally unusual, and I dare you to draw something with S4 symmetry.
Oh, all right. I'll do it.
The molecule below is 1,3,5,7-tetrafluorocyclooctatetraene. It has deceptively few symmetry elements: only one C2 rotation axis, no perpendicular C2' axes, no centre of inversion, and no mirror planes. With the absence of both i and σ you would initially expect the complex to be chiral. However, the compound possesses an S4 improper rotation axis, and so belongs to the S4 point group. Thus, the molecule is not chiral! The mirror images below are the same molecule, not enantiomers.
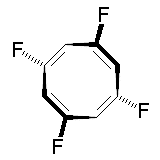
|
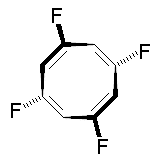
|
| How to Spot a Chiral Compound - Summary |
So, how do you tell if a molecule is chiral? There are two guaranteed methods, and a series of quick-and-dirty rules, increasing in their sophistication, precision, and difficulty of application.
• Method One: draw the mirror image. A chiral compound, by definition, is non-superimposable on its mirror, so that the mirror images are enantiomers. Draw or build the mirror image, and compare -- it must be either the same achiral structure or a new enantiomer.
• Method Two: find the point group. Only molecules belonging to Cn (which includes E) and Dn point groups are chiral, because only these groups lack the Sn element.
The first method is tedious and often difficult. The second is usually pretty straightforward, and it's what I do if the first two tricks below don't immediately hand me the answer.
• Rule One (limited): A compound is chiral if it has four different bonds to carbon.
• Rule Two (good): A compound is chiral if it lacks a mirror plane.
• Rule Three (better): A compound is chiral if it lacks both σ and i.
• Rule Four (infallible): A compound is chiral if it lacks an Sn axis.
The first rule is very fast, but only applies to organic compounds with a single stereocentre.
The second rule is also very fast, and applies to almost anything. The Ci and even-value Sn point groups break this rule, but those are exceedingly rare.
The third rule is harder to sort out, and while the fourth is the only one that always works, it's scary -- most people can't find improper rotation axes when they are present, let alone conclusively demonstrate their absence. If I'm not certain Rule Two is working, then I find it much easier and more reliable simply to assign the point group, which guarantees the correct answer.
This page is maintained and copyright by W. Stephen McNeil at UBC Okanagan.
.